Giải bài tập trang 62, 63 bài 2 Định lí đảo và hệ quả của định lí Talet Sách giáo khoa toán 8 tập 2. Câu 6: Tìm các cặp đường thẳng song song trong hình 13 và giải thích vì sao chúng song song...
Bạn đang xem: Sách toán 8 tập 2
Bài 6 trang 62 - Sách giáo khoa toán 8 tập 2
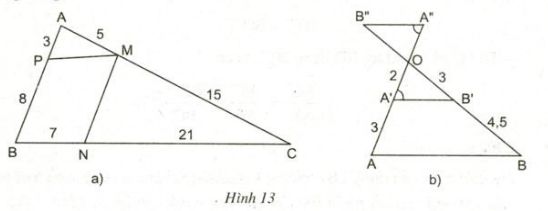
Tìm các cặp đường thẳng song song trong hình 13 và giải thích vì sao chúng song song.
Giải:
Trên hình 13a ta có:
\(\frac{AP}{PB}\) = \(\frac{3}{8}\); \(\frac{AM}{MC}\)= \(\frac{5}{15}\) = \(\frac{1}{3}\) vì \(\frac{3}{8}\) ≠ \(\frac{1}{3}\) nên \(\frac{AP}{PB}\) ≠ \(\frac{AM}{MC}\) => PM và MC không song song.
Ta có \(\left.\begin{matrix} &\frac{CN}{NB}=\frac{21}{7}=3 \\ & \frac{CM}{MA}=\frac{15}{5}=3 \end{matrix}\right\} => \frac{CM}{MA}=\frac{CN}{NB}\) => MN//AB
Trong hình 13b
Ta có: \(\frac{OA"}{A"A}\) = \(\frac{2}{3}\); \(\frac{OB"}{B"B}\) = \(\frac{3}{4,5}\) = \(\frac{2}{3}\)
=> \(\frac{OA"}{A"A}\) = \(\frac{OB"}{B"B}\) => A"B" // AB (1)
Mà \(\widehat{B"A"O}\) = \(\widehat{OA"B"}\) lại so le trong
Suy ra A"B" // A"B" (2)
Từ 1 và 2 suy ra AB // A"B" // A"B"
Bài 7 trang 62 - Sách giáo khoa toán 8 tập 2
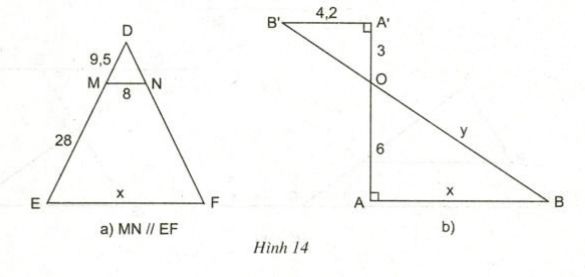
Tính các độ dài x,y trong hình 14.
Giải:
* Trong hình 14a
MN // EF => \(\frac{MN}{EF}\) = \(\frac{MD}{DE}\)
mà DE = MD + ME = 9.5 + 28 = 37.5
Nên \(\frac{8}{x}\) = \(\frac{9,5}{37,5}\) => x= \(\frac{8.37.5}{9.5}\) = \(\frac{600}{19}\) ≈ 31,6
* Trong hình 14b
Ta có A"B" ⊥ AA"(gt) và AB ⊥ AA"(gt)
=> A"B" // AB => \(\frac{A"O}{OA}\) = \(\frac{A"B"}{AB}\) hay \(\frac{3}{6}\) = \(\frac{4,2}{x}\)
x = \(\frac{6.4,2}{3}\) = 8.4
∆ABO vuông tại A
=> OB2 = y2 = OA2 + AB2
=> y2 = 62+ 8,42
=> y2 = 106,56
=> y ≈ 10,3
Bài 8 trang 63 - Sách giáo khoa toán 8 tập 2
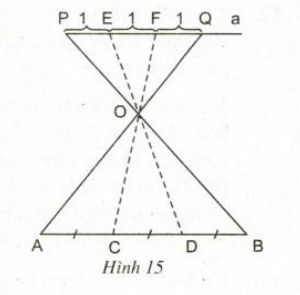
a) Để chi đoạn thẳng AB thành ba đoạn bằng nhau, người ta đã làm như hình 15.
Hãy mô tả cách làm trên và giải thích vì sao các đoạn AC,CD,DB bằng nhau?
b) Bằng cách tương tự, hãy chi đoạn thẳng AB cho trước thành 5 đoạn bằng nhau. Hỏi có cách nào khác với cách làm trên mà vẫn có thể chia đoạn AB cho trước thành 5 đoạn bằng nhau?
Giải:
a) Mô tả cách làm:
Vẽ đoạn PQ song song với AB. PQ có độ dài bằng 3 đơn vị
- Xác định giao điểm O của hai đoạn thẳng PB và QA.
- Vẽ các đường thẳng EO, FO cắt AB tại C và D.
Chứng minh AC=CD=DB
∆OPE và ∆OBD có PE//DB nên \(\frac{DB}{PE}\) = \(\frac{OD}{OE}\) (1)
∆OEF và ∆ODC có PE // CD nên \(\frac{CD}{EF}\) = \(\frac{OD}{OE}\) (2)
Từ 1 và 2 suy ra:
\(\frac{DB}{PE}\) = \(\frac{CD}{EF}\) mà PE = EF nên DB = CD.
Chứng minh tương tự: \(\frac{AC}{DF}\) = \(\frac{CD}{EF}\) nên AC = CD.
Vây: DB = CD = AC.
b) Tương tự chia đoạn thẳng AB thành 5 đoạn bằng nhau thực hiện như hình vẽ sau:
Ta có thể chia đoạn thẳng AB thành 5 đoạn thẳng bằng nhau như cách sau:
Vẽ 6 đường thẳng song song cách đều nhau( có thể dùng thước kẻ để vẽ liên tiếp). Đặt đầu mút A và B ở hai đường thẳng ngoài cùng thì các đường thẳng song song căt AB chia thành 5 phần bằng nhau.
Bài 9 trang 63 - Sách giáo khoa toán 8 tập 2
Cho tam giác ABC và điểm D trên cạnh AB sao cho AD= 13,5cm, DB= 4,5cm. Tính tỉ số các khoảng cách tự điểm A và B đến cạnh AC
Giải:
Gọi DH và BK lần lượt là khoảng cách từ B và D đến cạnh AC.
Ta có DH // BK (cùng vuông góc với AC)
=> \(\frac{DH}{BK}\) = \(\frac{AD}{AB}\)
Mà AB = AD + DB
=> AB = 13,5 + 4,5 = 18 (cm)
Vậy \(\frac{DH}{BK}\) = \(\frac{13,5}{18}\) = \(\frac{3}{4}\)
Vậy tỉ số khoảng cách từ điểm D và B đến AC bằng \(\frac{3}{4}\)
Bài 10 trang 63 - Sách giáo khoa toán 8 tập 2
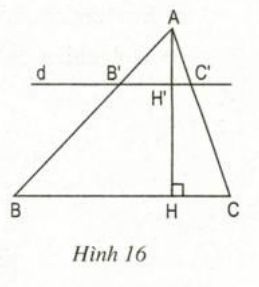
Tam giác ABC có đường cao AH. Đường thẳng d song song với BC, cắt các cạnh AB,AC và đường cao AH theo thứ tự tại các điểm B", C" và H"(h.16)
a) Chứng minh rằng:
\(\frac{AH"}{AH}\) = \(\frac{B"C"}{BC}\).
b) Áp dụng: Cho biết AH" = \(\frac{1}{3}\) AH và diện tích tam giác ABC là 67.5 cm2
Tính diện tích tam giác AB"C".
Xem thêm: Xem Phim Nước Mắt Cupid Tập 1 Vietsub, Stupid Cupid (2015), Nước Mắt Cupid
Giải:
a) Chứng minh \(\frac{AH"}{AH}\) = \(\frac{B"C"}{BC}\)
Vì B"C" // với BC => \(\frac{B"C"}{BC}\) = \(\frac{AB"}{AB}\) (1)
Trong ∆ABH có BH" // BH => \(\frac{AH"}{AH}\) = \(\frac{AB"}{BC}\) (2)
Từ 1 và 2 => \(\frac{B"C"}{BC}\) = \(\frac{AH"}{AH}\)
b) B"C" // BC mà AH ⊥ BC nên AH" ⊥ B"C" hay AH" là đường cao của tam giác AB"C".
Áp dụng kết quả câu a) ta có: AH" = \(\frac{1}{3}\) AH
\(\frac{B"C"}{BC}\) = \(\frac{AH"}{AH}\) = \(\frac{1}{3}\) => B"C" = \(\frac{1}{3}\) BC
=> SAB’C’= \(\frac{1}{2}\) AH".B"C" = \(\frac{1}{2}\).\(\frac{1}{3}\)AH.\(\frac{1}{3}\)BC