Tài liệu Giáo viên
Lớp 2Lớp 2 - liên kết tri thức
Lớp 2 - Chân trời sáng tạo
Lớp 2 - Cánh diều
Tài liệu Giáo viên
Lớp 3Lớp 3 - liên kết tri thức
Lớp 3 - Chân trời sáng tạo
Lớp 3 - Cánh diều
Tài liệu Giáo viên
Lớp 4Sách giáo khoa
Sách/Vở bài tập
Tài liệu Giáo viên
Lớp 5Sách giáo khoa
Sách/Vở bài bác tập
Tài liệu Giáo viên
Lớp 6Lớp 6 - liên kết tri thức
Lớp 6 - Chân trời sáng tạo
Lớp 6 - Cánh diều
Sách/Vở bài xích tập
Tài liệu Giáo viên
Lớp 7Lớp 7 - kết nối tri thức
Lớp 7 - Chân trời sáng tạo
Lớp 7 - Cánh diều
Sách/Vở bài bác tập
Tài liệu Giáo viên
Lớp 8Sách giáo khoa
Sách/Vở bài xích tập
Tài liệu Giáo viên
Lớp 9Sách giáo khoa
Sách/Vở bài xích tập
Tài liệu Giáo viên
Lớp 10Lớp 10 - kết nối tri thức
Lớp 10 - Chân trời sáng tạo
Lớp 10 - Cánh diều
Sách/Vở bài xích tập
Tài liệu Giáo viên
Lớp 11Sách giáo khoa
Sách/Vở bài tập
Tài liệu Giáo viên
Lớp 12Sách giáo khoa
Sách/Vở bài tập
Tài liệu Giáo viên
thầy giáoLớp 1
Lớp 2
Lớp 3
Lớp 4
Lớp 5
Lớp 6
Lớp 7
Lớp 8
Lớp 9
Lớp 10
Lớp 11
Lớp 12

Lý thuyết, những dạng bài xích tập Toán 8Toán 8 Tập 1I. Lý thuyết & trắc nghiệm theo bàiII. Các dạng bài xích tậpI. Triết lý & trắc nghiệm theo bàiII. Các dạng bài tậpToán 8 Tập 1I. Triết lý & trắc nghiệm theo bài xích họcII. Các dạng bài bác tập
Tổng hợp các cách chứng tỏ bất đẳng thức hay, chi tiết
Với Cách minh chứng bất đẳng thức hay, cụ thể môn Toán lớp 8 phần Đại số để giúp học sinh ôn tập, củng cố kỹ năng từ đó biết phương pháp làm những dạng bài bác tập Toán lớp 8 Chương 4: Bất phương trình số 1 một ẩn để được điểm cao trong các bài thi môn Toán 8.
Bạn đang xem: Chứng minh bất đẳng thức lớp 8
Dạng 1: Sử dụng chuyển đổi tương đương
A. Phương thức giải
Một số kĩ thuật cơ bản:
+ kỹ thuật xét hiệu nhị biểu thức
+ nghệ thuật sử dụng các hằng đẳng thức
+ chuyên môn thêm sút một hằng số, một biểu thức
+ kỹ thuật đặt trở thành phụ
+ Kỹ thuật sắp tới thứ tự những biến.
+ Kỹ thuật khai quật tính bị chặn của những biến
B. Lấy ví dụ minh họa
Câu 1: mang đến a với b là nhị số bất kỳ chứng minh rằng
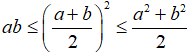
Lời giải:
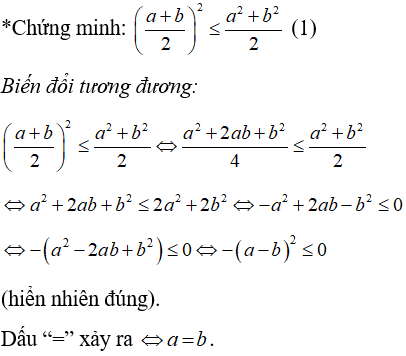
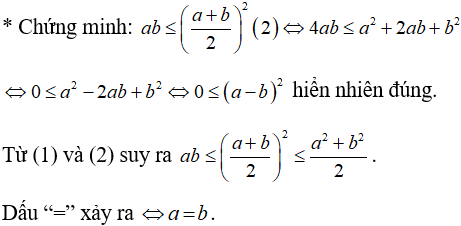
Câu 2:
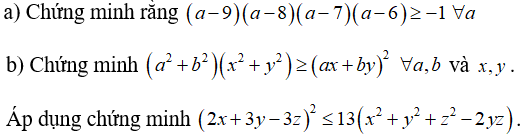
Lời giải:
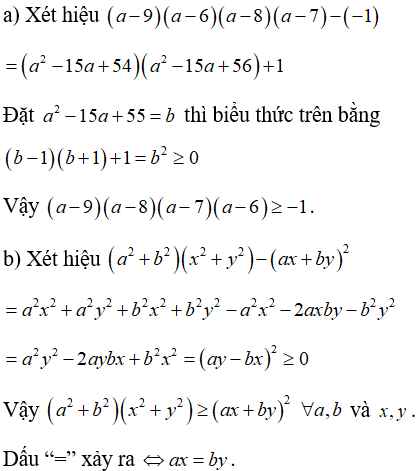
Áp dụng:
Ta viết bất đẳng thức
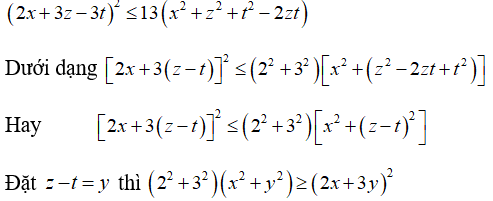
đúng theo bất đẳng thức vừa chứng tỏ ở trên.
Câu 3: minh chứng rằng với tía số a,b,c tùy ý ta luôn luôn có:
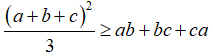
Lời giải:
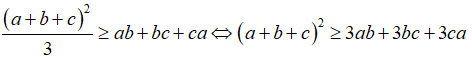
Xét hiệu:
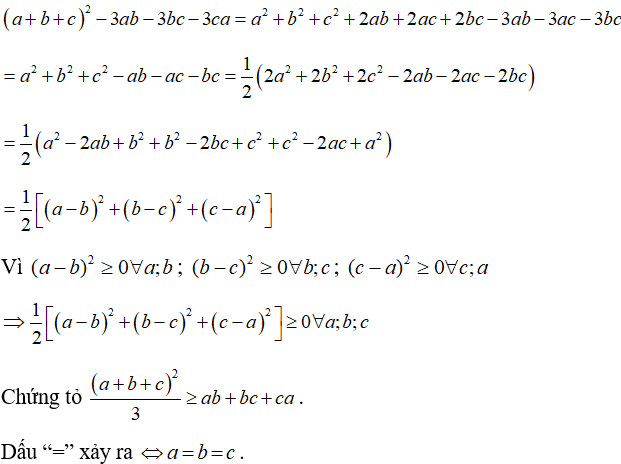
C. Bài xích tập tự luyện
Câu 1: mang lại a, b, c là những số thực bất kì. Chứng minh rằng:
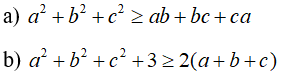
Câu 2: đến a, b, c là các số thực bất kì. Chứng tỏ rằng:
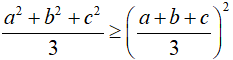
Câu 3: mang lại a, b, c, d, e là các số thực bất kì. Minh chứng rằng:
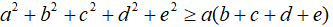
Câu 4: đến a, b, c là những số thực vừa lòng điều kiện a, b, c ≥1. Chứng tỏ rằng:
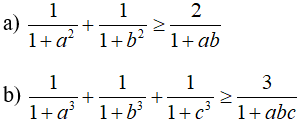
Câu 5: cho a, b, c là những số thực dương thỏa mãn
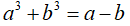
Chứng minh rằng:
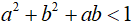
Câu 6: cho các số thực a, b, c vừa lòng điều kiện a+b+c=0 .
Chứng minh rằng
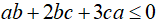
Câu 7: mang đến a, b, c là các số thực dương tùy ý. Chứng tỏ rằng:
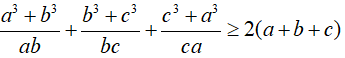
Câu 8: minh chứng rằng với đa số số thực không giống không a, b ta có:
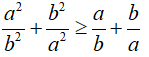
Dạng 2: Sử dụng cách thức phản chứng
A. Phương thức giải
+ cần sử dụng mệnh đề đảo
+ phủ định rồi suy ra điều trái với mang thiết
+ đậy định rồi suy ra trái với điều đúng
+ bao phủ định rồi suy ra nhị mệnh đề trái ngược nhau
+ tủ định rồi suy ra kết luận
*Một số đẳng thức và bất đẳng thức cần nhớ:
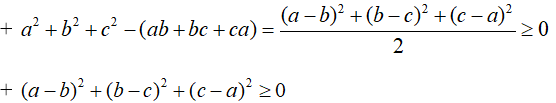
B. Ví dụ như minh họa
Câu 1: minh chứng rằng:
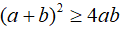
Lời giải:
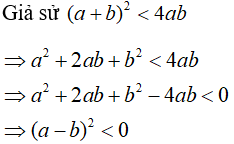
Điều này là vô lý với tất cả a cùng b
Vậy điều đưa sử là không nên →điều bắt buộc chứng minh.
Câu 2: Cho tía số a, b, c ∈ (0;1) . Chứng tỏ rằng có ít nhất một trong các bất đẳng thức sau đấy là sai:
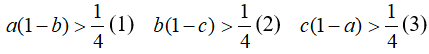
Lời giải:
Giả sử cả tía bất đẳng thức trên đều đúng. Theo giả thiết a, b, c, 1-a, 1-b, 1-c mọi là số dương suy ra
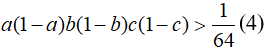
Mặt khác:

Câu 3: cho a, b, c là các số thực vừa lòng các đk sau:
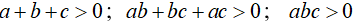
Chứng minh rằng cả tía số a, b, c hồ hết là số dương.
Lời giải:
Giả sử rằng trong tía số a, b, c có một số trong những không dương, ko mất bao quát ta lựa chọn số đó là a, tức là a≤0.
Xem thêm: Thuốc Giảm Cân 30 Day Diet 60 Viên Của Mỹ, 30 Day Diet
Vì abc>0 buộc phải a≠0, do đó suy ra aa) chứng minh rằng với đa số số thực a, b ta bao gồm |a ± b| ≥ |a| - |b|.b) biết rằng | a | > 2 | b |. Minh chứng rằng |a|